Методы математического моделирования задач ОМД
Особым классом задач исследований поведения материалов, являются задачи обработки металлов давлением, в которых требуется учитывать нелинейный характер взаимосвязи между напряжениями и деформациями в пластической области, что в существенной мере усложняет решение по сравнению с другими областями механики. Современный подход к решению задач ОМД – использование метода конечных элементов (МКЭ). Значительным преимуществом МКЭ является возможность моделирования деформационных нестационарных процессов. МКЭ позволяет с большой точностью исследовать динамику и кинематику деформационных процессов в любой части исследуемой области с учетом реологических особенностей деформируемых материалов как гомогенного, так и гетерогенного строения. В отличие от аналитических методов МКЭ дает возможность строить более совершенные математические модели, в том числе и объемные, основанные на значительно меньшем числе допущений и ограничений. Поэтому результаты исследований, полученные с его помощью, более объективны. МКЭ представляет собой весьма универсальный метод, имеющий простую физическую основу и математическую форму, которая реализуется с помощью гибкого алгоритма, хорошо приспособленного для решения на ЭВМ.
Решение реальных 3D задач пластического деформирования требует разбиения очага деформации на несколько десятков, а то и сотен тысяч конечных элементов с автоматической перестройкой сетки элементов на каждом шаге по времени. Для обеспечения этой возможности ресурсы вычислительной техники по объемам памяти и быстродействию должны характеризоваться цифрами, которые еще вчера были уделом рабочих станций, т.е. практически не доступной для технолога техники.
На кафедре «ТОМД» накоплен большой опыт применения программ математического моделирования для анализа пластического формоизменения гомогенных и гетерогенных материалов в процессах ОМД. Решаются задачи исследования пластического течения металлов в процессах прокатки, прессования, волочения, гибки и объемной штамповки. Для моделирования используются современные программные конечно-элементные программные продукты QForm и DeForm, предназначенные непосредственно для решения задач ОМД и универсальный конечно-элементный пакет Ansys-DYNA для моделирование формоизменения гетерогенных материалов.
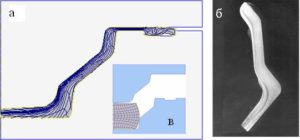
В частности, проведено исследование возможности управления структурой и свойствами штампованных поковок из алюминиевых сплавов при производстве деталей типа «фланец» методом горячей штамповки. Данные изделия широко используются в качестве переходников топливных систем. В соответствии с типовым технологическим процессом подобные изделия следует получать многопереходной объемной штамповкой в закрытых ручьях. Однако переходники относятся к мелкосерийному производству и изготовление многоручьевых закрытых штампов не всегда бывает целесообразным. В этой связи, с использованием математического моделирования в среде QForm, разработан новый научно обоснованный технологический процесс получения подобных изделий однопереходной горячей штамповкой. В ходе исследования проводилось моделирование течения металла в ручье штампа в зависимости от геометрических параметров заготовки и реализуемой схемы деформированного состояния. Так было получено, что при штамповке по схеме обратного выдавливания в полученной поковке наблюдается (рис.1) смещение слоев металла с наибольшей накопленной деформацией во внешние зоны поковки, где в дальнейшем они будут удалены механической обработкой и требуемый эффект упрочнения достигнут не будет.
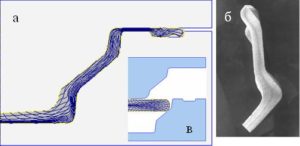
При штамповке по схеме вытяжки удалось получить поковку с зоной максимальной деформации находящейся в контуре чистового изделия (рис.2).
-
Рис. 1. Распределение деформации по объёму штампованной поковки при её формообразовании путём обратного выдавливания.
а. Результаты математического моделирования;
б. Макроструктура сечения штамповки фланца;
в. Положение заготовки в штампах.
-
Рис.2. Распределение деформации по объёму штампованной поковки при её формообразовании путём последовательной вытяжки.а. Результаты математического моделирования;
б. Макроструктура сечения штамповки фланца;
в. Положение заготовки в штампах.
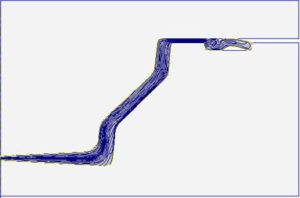
- Рис.3. Распределение деформации по объёму штамповки при её формообразовании вытяжкой, предварительного фасонирования в конических бойках, и отказе от дополнительных припусков.
Следующая рассматриваемая задача – моделирование процесса прессования через язычковую матрицу. Сложность математического моделирования заключается в особенностях течения металла при использовании язычковой матрицы. В этом случае, в очаге деформации, истекающий материал разделяется на два потока, огибает иглу матрицы, а затем сваривается под высоким давлением в рабочем пояске. Для задач математического моделирования процессов ОМД процесс сваривания не характерен, к тому же в программах моделирования деформируемый материал как правило задается сплошной неразрывной средой, и эффект разделения материала и последующее его смыкание они интерпретируют, как появление зажима. Поэтому для данной задачи необходимо использовать те средства моделирования, где программно реализована возможность сваривания материала в очаге деформации. Расчет прессования через язычковую матрицу выполнен в программе DeForm (рис.4). В результате получена модель и исследован анализ течения материала через профиль матрицы.
Расчет скоростей истечения металла при прессовании в матрицу позволил сконструировать оптимизированную матрицу с переменной величиной рабочего пояска, с целью получения равномерного распределения полей скоростей (рис.5).
- Рис.4. Прессование через язычковую матрицу.а. К.Э. модель прессования с язычковой матрицей; а. Расчет скорости истечения металла через матрицу.
- Рис. 5. Распределение полей скоростей истечения металла при прессовании в оптимизированную матрицу.
Совершенно иным классом задач является, моделирование процессов формоизменения гетерогенных материалов. Исторически кафедра уже более 30 лет занимается получением изделий и волокнистых композиционных материалов (ВКМ) методами ОМД. Особенностью данных материалов является сочетание пластичной матричной составляющей и жесткого упрочняющего волокна. Стандартные пакеты программ для моделирования технологических процессов ОМД в этом случае мало применимы, либо применимы с очень большими допущениями, что делает полученные результаты поверхностными. В этом случае целесообразно использовать универсальные конечно-элементные программы, как, например ANSYS-DYNA.
В настоящее время наблюдается востребованность в конструкционных силовых элементах большой прочности и малой массы. Для этих целей могут быть применены гнутые профили и оболочки из ВКМ системы AL-B. Получение этих изделий связано с проектированием многофакторного технологического процесса, основанного на критериальных подходах. Оценить вклад каждого из факторов (температуры, деформации, времени процесса и т.п.) можно используя средства моделирования.
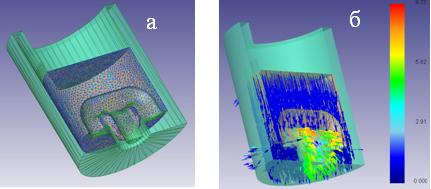
В среде ANSYS-DYNA построены конечно-элементные математические модели заготовок изделий ВКМ (рис.6) под последующую гибку и обкатку.
- Рис.6. К.Э. модель заготовки ВКМ.
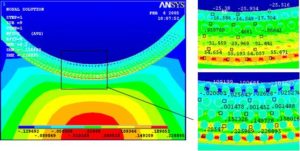
- Рис.7. Напряжения в очаге деформации при гибке.
В результате моделирование позволило для процесса гибки профилей из ВКМ определить минимально допустимый относительный радиус гиба, максимальные растягивающие напряжения (рис.7), а также сформулировать основные функциональные зависимости обеспечивающие получение изделия требуемого качества.
Исследование процесса обкатки (рис.8) позволило определить величины требуемого усилия и скорости, описать параметры очага деформации и в результате сформулировать функциональную зависимость усилия компактирования от параметров заготовки при заданной скорости, температуре и среде.
-
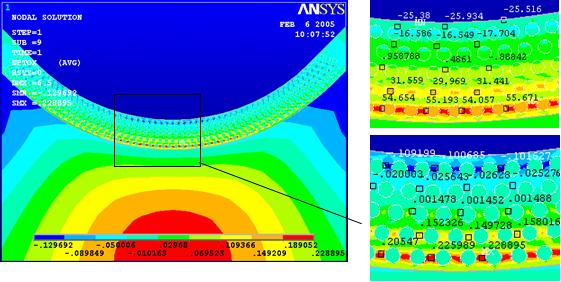
Рис.8. Моделирование обкатки оболочек из ВКМ.
а. Определение усилия прижима валка;
б. Моделирование распространения напряжения при движении валка;
в. Напряжения компактирования в очаге деформации.
Проделанная работа говорит о том, что уже сегодня современный персональный компьютер вполне пригоден для моделирования пластической деформации заготовок гетерогенного строения, многопереходных процессов штамповки, прокатки, прессования и иных процессов ОМД.